√1000以上 x^y y^x=2 find dy/dx 208234-Example 9 if x^(y)+y^(x)=2 find (dy)/(dx)

Solution for Solve dy/dx=2xy/(x^2y^2) Q A group of 150 tourists planned to visit East AfricaAmong them, 3 fall ill and did not come, of th A Consider the provided question, First draw the Venn diagram according to the given question, Let K r I'll start with the second one for you Take the natural logarithm of both sides ln(x^y * y^x) = ln(1) ln(x^y) ln(y^x) = 0 yln(x) xln(y) = 0 dy/dxln(x) y/x ln y x/y(dy/dx) = 0 dy/dx(lnx x/y) = lny y/x dy/dx= (lny y/x)/(lnx x/y) dy/dx= (ln y y/x)/(lnx x/y) Now for the second I would differentiate term by term Let t = x^y and u = y^x Then lnt = ln(x^y) and lnu#mathematic #preumath #iium #calculus안녕하세요, this is my video for teaching calculus i will make more problem solving videos soon Stay tuned😘🧸I wanna help

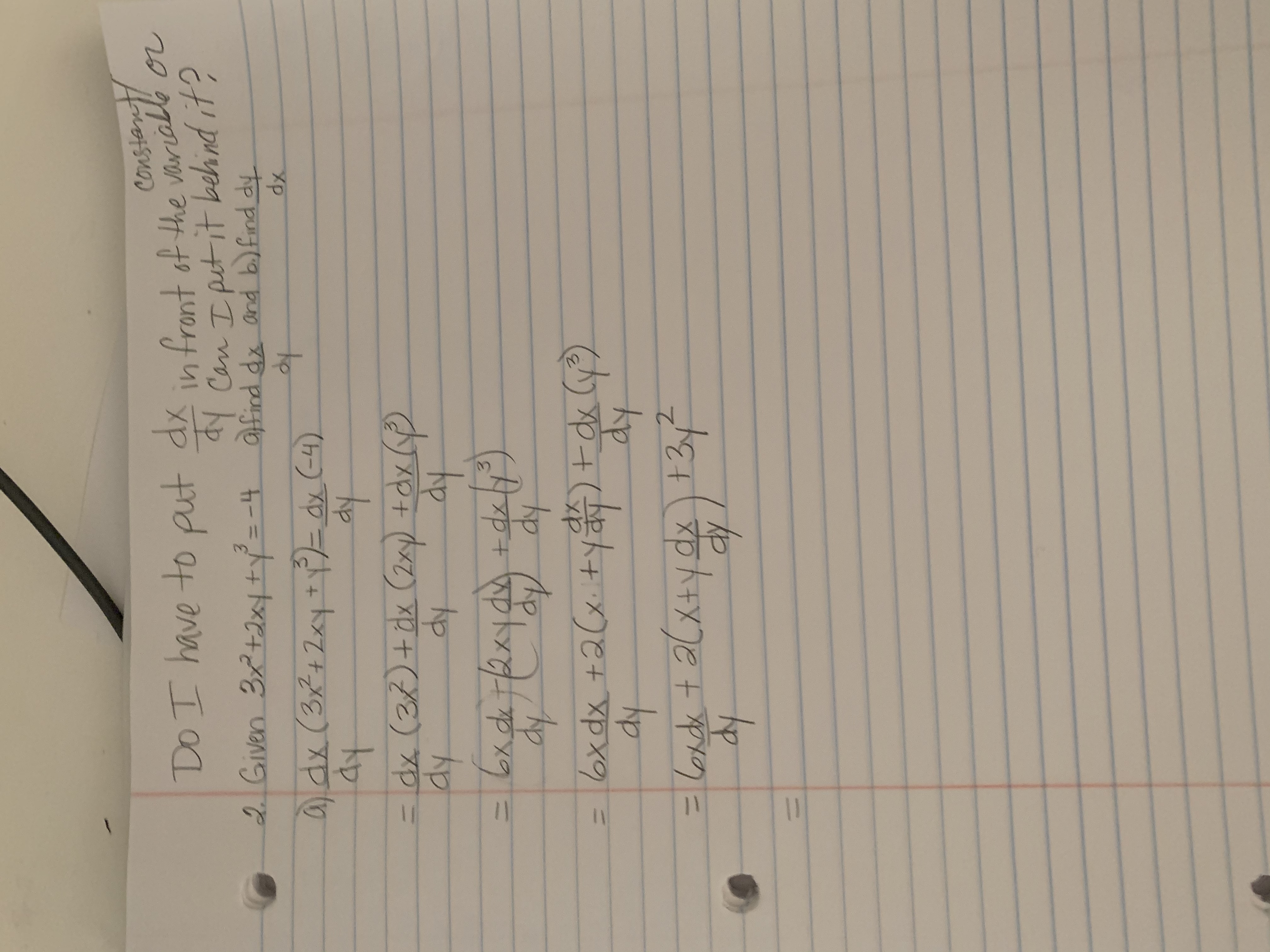
Answered Rebecca Ferrer 2 26 Given Bartleby

Example 9 if x^(y)+y^(x)=2 find (dy)/(dx)

Example 9 if x^(y)+y^(x)=2 find (dy)/(dx)- If x = a(cosθ logtanθ/2), y = asinθ , find dy/dx at θ = π/4 asked in Continuity and Differentiability by KumkumBharti ( 539k points) continuityThe equation of the plane passing through the point (1, 2, − 3) and perpendicular to the planes 3 x y − 2 z = 5 and 2 x − 5 y − z = 7, is View solution If the least and the largest real values of α for which the equation z α ∣ z − 1 ∣ 2 i = 0 ( z ∈ C and i = − 1 ) has a solution are p and q respectively;

Scholarspace Manoa Hawaii Edu Bitstream Differentialequations Pdf

 Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at TeachooView Full Answer Hello Abhi dear, really challenging one you know!Calculus Find dy/dx y=x^2e^x y = x2ex y = x 2 e x Differentiate both sides of the equation d dx (y) = d dx (x2ex) d d x ( y) = d d x ( x 2 e x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps

Now the given equation is (x2 y2)2 = xyOr, (x2)2 2xy (y2)2 = xy→ x4 xy y4 = 0Differentiating the above expression wrt x, we get4x3 xdxdy y 4y3 dxdy = 0dxdy (x4y3)= −(y4x3)∴ dxdyAnswer x^(y1) y y^x logy/1 x^y logx x y^(x1) Solution y = x^y y^x Let u = x^y and v = y^x Then, y = u v and dy/dx = du/dx dv/dxF(x,y)=3x2 2xy 4y3 Answer dy dx = − f x f y = − 6x2y 12y2 2x 5 f(x,y)=12x5 −2y Answer dy dx = − f x f y = − 60x4 −2 =30x4 6 f(x,y)=7x2 2xy2 9y4 Answer dy dx = − f x f y = − 14x2y2 36y3 4xy Example 11 For f(x,y,z) use the implicit function theorem to find dy/dx and dy/dz 1 f(x,y,z)=x 2y3 z xyz Answer dy dx

 x^y y^x= 2 Find dy/dx Share with your friends Share 0 dy/dx = 0 0 ;(xy)² dy/dx=a² =>dy/dx=a²/(x–y)² Let (x–y)=z so that 1– dy/dx = dz/dx => dy/dx = 1– dz/dx Then, put dy/dx = 1– dz/dx in above differential equation 1Ln(xy)= xy LnxLny= xy Lnyy=xLnx DLnyydx=DxLnxdx (1/y)dy/dxdy/dx= 1(1/x) Factor out dy/dx dy/dx(1/y 1)= 1(1/x) dy/dx= (1(1/x))/((1/y)1) Combine like terms if you care to make it aesthetically neat, concise, and symmetrical dy/dx= ((x1)/x)/((1y)/y dy/dx= y(x1)/x(1y)

1

Use Implicit Differentiation To Find Dy Dx Xy 4 Chegg Com

Find dy/dx by implicit differentiationxy x y = x2y2 asked in Mathematics by BrownBoa calculus Find dy/dx by implicit differentiationxy x = 2 asked in Mathematics by Jesuscourted finiteanddiscretemath Use implicit differentiation to find dy/dxcos xy x6 = y6Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more Transcript Ex 53, 5 Find 𝑑𝑦/𝑑𝑥 in, 𝑥2 𝑥𝑦 𝑦2 = 100 𝑥2 𝑥𝑦 𝑦2 = 100 Differentiating both sides 𝑤𝑟𝑡𝑥

Solve Dy Dx 1 X Y Solve Dy Dx Y X 1 Y Solve The Chegg Com

Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf

Verify that y = e^(m cos^(1)) x is a solution of the differential equation (1 x^2)d^2 y/dx^2 x(dy/dx) m^2y = 0 asked May 10 in Differential Equations by Yajna ( If x y y x = 2 then find dy/dx differentiation;How can I solve dy/dx=xy/xy?

If X Y Y X What Is Dy Dx Quora

Find Dy Dx If Y X 1 X 2

Then 4 ( p 2 q 2 ) is equal to ________Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreFind dy/dx given x^3 3 x^2 y 2 x y^2 = 12 WolframAlpha Have a question about using WolframAlpha?

Find Dy Dx Y X 2 1 3 2x 1 Sqrt X 3 4x 1

2 6 Webassign Answers

Reuven Harmelin, Lecturer at Technion Israel Institute of Technology (19present) Updated 4 years ago Author has 774 answers and 3964K answer views The equation in your question actually defines two different functions ("d"y)/("d"x)y/x=xy^2 Divide both sides by y^2 y^2 ("d"y)/("d"x)1/(xy)=x Then, define a function v=y^(12)=y^1 Differentiate both sides with respect to x to get ("d"v)/("d"x)=("d"y)/("d"x)y^2, or ("d"y)/("d"x)=y^2("d"v)/("d"x)Solve differential equation (dy/dx) (y/x) = x^2 If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history and influence TV

Implicit Differentiation

Question 1 Find Dy Dx A Y X 3x Ver B Chegg Com

Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreBy the Sum Rule, the derivative of x 2 y 2 x 2 y 2 with respect to x x is d d x x 2 d d x y 2 d d x x 2 d d x y 2 d d x x 2 d d x y 2 d d x x 2 d d x y 2 Differentiate using the Power Rule which states that d d x x n d d x x n is n x n − 1 n x n 1 where n = 2 n = 2 x^2y^2=c dy/{dx}=x/y ydy=xdx by exploiting the notation (separation) int ydy=int xdx further exploiting the notation 1/2y^2=1/2x^2d y^2=x^22d x^2y^2=2d x^2y^2=c where c=2d Depending on whether c is positive, negative or zero you get a hyperbola open to the xaxis, open to the y=axis, or a pair of straight lines through the origin

Second Derivatives Implicit Equations Find Expression Video Khan Academy

Solved Find The Derivative Of Y 3 X 2 3 X 3284

 Ex 96, 3 For each of the differential equation given in Exercises 1 to 12, find the general solution 𝑑𝑦﷮𝑑𝑥﷯ 𝑦﷮𝑥﷯= 𝑥﷮2﷯ 𝑑𝑦﷮𝑑𝑥﷯ 𝑦﷮𝑥﷯= 𝑥﷮2﷯ Differential equation is of the form 𝑑𝑦﷮𝑑𝑥﷯𝑃𝑦=𝑄 where P = 1﷮𝑥﷯ and Q = x2 Finding integrating factor, IF = e﷮ ﷮﷮𝑝 𝑑𝑥﷯﷯ IF = e﷮The issue is that you integrated y with respect to x, and concluded that it was equal to y This is only viable if y = aex for some constant a, which we have no reason to suspect Solve y ^2x (\frac {dy} {dx})^2 = 1 using proposed change of variables Solve y2 −x(dxdy )2 = 1Let x^y = m and y^x = n Taking ln we have y ln x = ln m Differentiating wrt x we have (y/x) ln x *y' = 1/m * dm/dx Or dm/dx = x^y * (y/x) ln x * y' (1) Same way we can get

Find The Derivative For The Following Functions Find Chegg Com

Answered 3 7 Find The Second Partial Bartleby

Calculus Find dy/dx y = natural log of x^2 y = ln (x2) y = ln ( x 2) Differentiate both sides of the equation d dx (y) = d dx (ln(x2)) d d x ( y) = d d x ( ln ( x 2)) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equationFind dy/dx x^2= (xy)/ (xy) x2 = x y x y x 2 = x − y x y Differentiate both sides of the equation d dx (x2) = d dx (x y x y) d d x ( x 2) = d d x ( x − y x y) Differentiate using the Power Rule which states that d dxxn d d x x n is nxn 1 if y = log tan (∏/4 x/2) show that dy/dx = sec x donot go shortcut if y = log (x (1 x 2) 1/2) prove that dy/dx = 1/log(x (1 x 2) 1/2) 1/(1 x 2) 1/2;

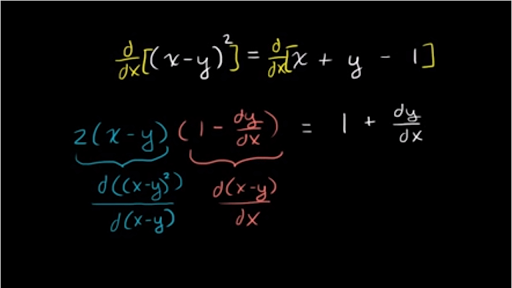
Worked Example Implicit Differentiation Video Khan Academy

Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection

Find dy/dx when y = x^2 (cos (x)) y = x 2 (cos (x)) therefore we will need to use the product rule, dy/dx = u dv/dx v du/dx where u = x 2 and v = cos (x) du/dx = 2x and dv/dx = sin (x), (don't forget the negative symbol when differentiating cosine) dy/dx = x 2 ( sin (x)) cos (x) (2x) dy/dx = 2x (cos (x)) x 2 (sin (x))Since 2 2 is constant with respect to x x, the derivative of 2 2 with respect to x x is 0 0 2 x 0 2 x 0 Add 2 x 2 x and 0 0 2 x 2 x 2x 2 x Reform the equation by setting the left side equal to the right side y' = 2x y ′ = 2 x Replace y' y ′ with dy dx d y d x dy dx = 2x d y d x = 2 xHow do you find dy/dx of y=tan^4 (x^22)?

4 2 Implicit Differentiation

Partial Differentiation Uia Logo Main Menu Prev Next Swin On This Page We Shall Solve The Same Task As On The Previous Page But This Time By Means Of A Function With Several Variables And Use Of Total Differential Originally We Had Given The Equation Y

 Ex 55, 12 Find 𝑑𝑦/𝑑𝑥 of the functions in, 𝑥^𝑦 𝑦^𝑥 = 1 𝑥^𝑦 𝑦^𝑥 = 1 Let 𝑢 = 𝑥^𝑦 , 𝑣 = 𝑦^𝑥 Hence, 𝑢𝑣=1 Differentiating both sides 𝑤𝑟𝑡𝑥 (𝑑(𝑣⁡〖 𝑢〗))/𝑑𝑥 = 𝑑(1)/𝑑𝑥 𝑑𝑣/𝑑𝑥 𝑑𝑢/𝑑𝑥 = 0 (Derivative of Explanation 2xy y2 = x y d dx(2xy y2) = d dx(x y) 2 d dx (xy) 2y d dx = 1 d dx Use product rule and finish it off to get 2(x d dx y) 2y d dx = 1 d dx to make it clearer, let d dx = y' so you get 2(xy' y) 2yy' = 1 y'Answer to Find dy/dx by implicit differentiation and evaluate the derivative at the given point (x_0, y_0) 2 x^3 y x y^2 = x, (x_0, y_0) = (1,

How Do You Find Dy Dx For Y 2x Sqrt X 1 Socratic

If X Y E X Y What Is Dy Dx Quora

How to find dy/dx by implicit differentiation given that xy = x yHere's the 4 simple steps we will take in order to find dy/dx from the given equation xyShare It On Facebook Twitter Email 1 Answer 1 vote answered by Nakul01 (369k points) selected by KumariMuskan Best answer Given, x y = y x Taking logarithm on both sides, we get yIf y = 2^x, find dy/dx Q If y = 2^x, find dy/dx ANSWER 1) Take Logs of both sides of our equation y = 2^x So we get log (y)=log (2^x) 2) Apply relevant log rule to rhs Log rule log (a^b) = b log (a) nb the dot between b and log (a) represents x / multiply / times ) So we get log (y) = x log (2)

Ii Use The Inverse Rule To Find Dy Dx 1 X Y Y2 Gauthmath

Differentiation The Derivative And The Tangent Line Problem Ppt Download

Y = (x^2)sin (3x) Find dy/dx We need to differentiate x 2 sin (3x) We know how to differentiate (x 2) on its own, and how to differentiate sin (3x) on its own So we can use the Product rule dy/dx = (d/dx (x 2 ))sin (3x) x 2 (d/dx (sin (3x)) = (2x)sin (3x) x 2 (3cos (3x))Multiply by y/y first Note from our relation 2y^2\log yx^2=0 that adding x^2 to both sides yields 2y^2\log y=x^2 Substitute for 2y^2\log y and you are done \begin {align*}\frac {dy} {dx}&=\frac {x} {2y\log yy}\\&=\frac {xy} {2y^2\log yy^2}\\&=\frac {xy} {x^2y^2}\end {align*} Multiply by y/y first Note from our relation 2y2 logy− x2 = 0 that adding x2 to both sides yields 2y2logy = x2Share It On Facebook Twitter Email 1 Answer 1 vote answered by ManishaBharti (650k points) selected by faiz Best answer u v = 2 => du/dx dv/dx = 0 here u = xy & v = yx ⇒ ln u = y ln x & ln v = x ln y

Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 2 solutions Pdf

Use Fourth Order Runge Kutta Method To Find The Value Of Y At X 1 Given That Dy Dx Y X Y X Such That Y 0 1 Taking H 0 5

Find $ \dfrac{dy}{dx} $ if $ y = 2u^2 3u $ and $ u = 4x 1 $ I am trying to use the chain rule on it $$ \dfrac{dy}{dx} = \dfrac{dy}{du} \dfrac{du}{dx} $$ My work so far $$ \dfrac{d}{du}(2u^23u) * \dfrac{d}{dx}(4x1) = (4u3)(4) $$ However I am not absolutely sure I am doing it right and I don't have the answer in my bookIf sin(xy) x/y = x2 y, then dy/dx is equal to Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Get an answer for 'If x y = xy, then dy/dx = Please explain step by step' and find homework help for other Math questions at eNotes

Q5 If X 2 Xy Y 2 100 Find Dy Dx Implicit Function If X2 Xy Y2 100 Find Dy Dx Youtube

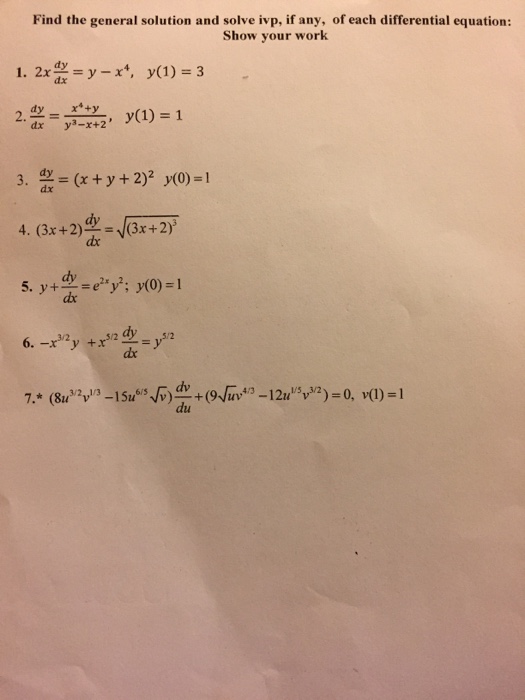
Find The General Solution And Solve Ivp If Any Of Chegg Com

 Solve the linear equation dy/dxy/x=x^2 Latest Problem Solving in Differential Equations More Questions in Differential Equations OnlineUsing these two ideas where y=e^(xlna) dy/dx = (lna)e^(xlna) now we can substitute in our initial expression y=a^x therefore dy/dx = (a^x)lna using this method, you can differentiate any function of the same form for example where y=2^x we can see that a=2 so dy/dx = 2^xln2Simple and best practice solution for (xx*y^2)dx(1x^2)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework

N3njeazobsm8bm

Ex 5 3 5 Find Dy Dx In X2 Xy Y2 100 Class 12

Find dy/dx y = x x e (2x 5) mention each and every step Find dy/dx (x) 1/2 (y) 1/2 = (a) 1/2 Mention each and every step If x y = y x, find dy/dx bseb model set;

Answered 1 Circle The Two Equations For Which Bartleby

Www Ualberta Ca Rjia Math215 Hwks Sol7 Pdf

Find Dy Dx By Implicit Differentiation X 2 Y 2 Chegg Com

Equation Xy Yx Wikipedia

Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection

Homogeneous Differential Equations

Q Tbn And9gcq9arl5ab K Kkztqdma6czzlslnfprp6ljv7o6a18 5qqda4yy Usqp Cau

If X Y Y X 2 Find Dy Dx

Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf

Find Dy Dx If Y X 2 1 X 2 1 Brainly In

If X Y Y X Then Find Dydx

Find Dy Dx When X And Y Are Connected By The Relation X2 Y2 2 Xy Studyrankersonline

Find Dy Dx For The Given Function Y X 1 X 2 X Brainly In

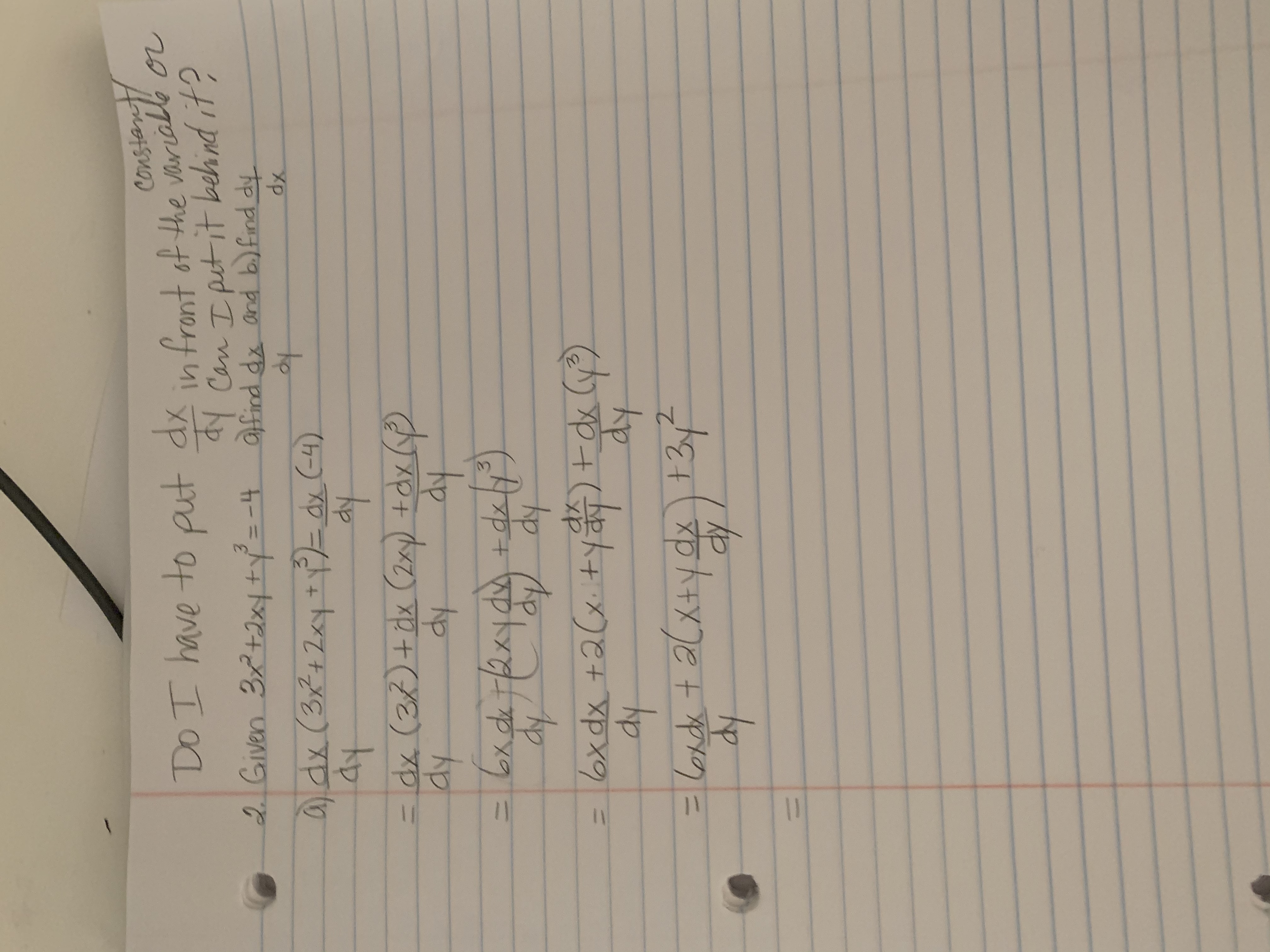
Answered Rebecca Ferrer 2 26 Given Bartleby

Scholarspace Manoa Hawaii Edu Bitstream Differentialequations Pdf

If Y Xcot X 2x2 3 X2 X 2 Find Dy Dx Mention Each And Every Step Mathematics Topperlearning Com Palrsebb

If Y X 2 2x 3x 4 Then Find Dy Dx

Ex 5 5 12 Find Dy Dx Xy Yx 1 Class 12 Cbse Ncert

If Sin Xy X Y X 2 Y Then Dy Dx Is Equal To Sarthaks Econnect Largest Online Education Community

Engineering Mathematics Notes

1

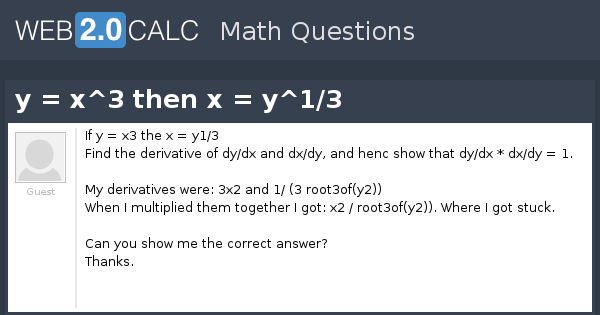
View Question Y X 3 Then X Y 1 3

If Y X What Is Dy Dx Quora

Double Integrals Over General Regions Page 2

If X Y Y X What Is Dy Dx Quora

Worked Example Implicit Differentiation Video Khan Academy

If Sin Xy X Y X 2 Y Find Dy Dx Brainly In

Www Usna Edu Users Oceano Raylee Sm223 Ch14 5 Stewart 16 Pdf

3 8 Implicit Differentiation Calculus Volume 1

Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Q4 Pdf

Solution Solve The Linear Equation Dy Dx Y X X 2

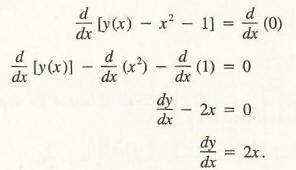
Find A Derivative With Step By Step Math Problem Solver

If Sin X Y Log X Y Then Dy Dx Youtube

For Each Of The Following Find Dy Dx Y X 3 E X Chegg Com

Find Dy Dx When X And Y Are Connected By The Relation Sin Xy X Y X2 Y Studyrankersonline

Solve Dy Dx Y X Log Y Y X 2 Log Y 2 Sarthaks Econnect Largest Online Education Community

Scholarspace Manoa Hawaii Edu Bitstream Differentialequations Pdf

Find Y For Ln X Y Arctan Xy Mathematics Stack Exchange

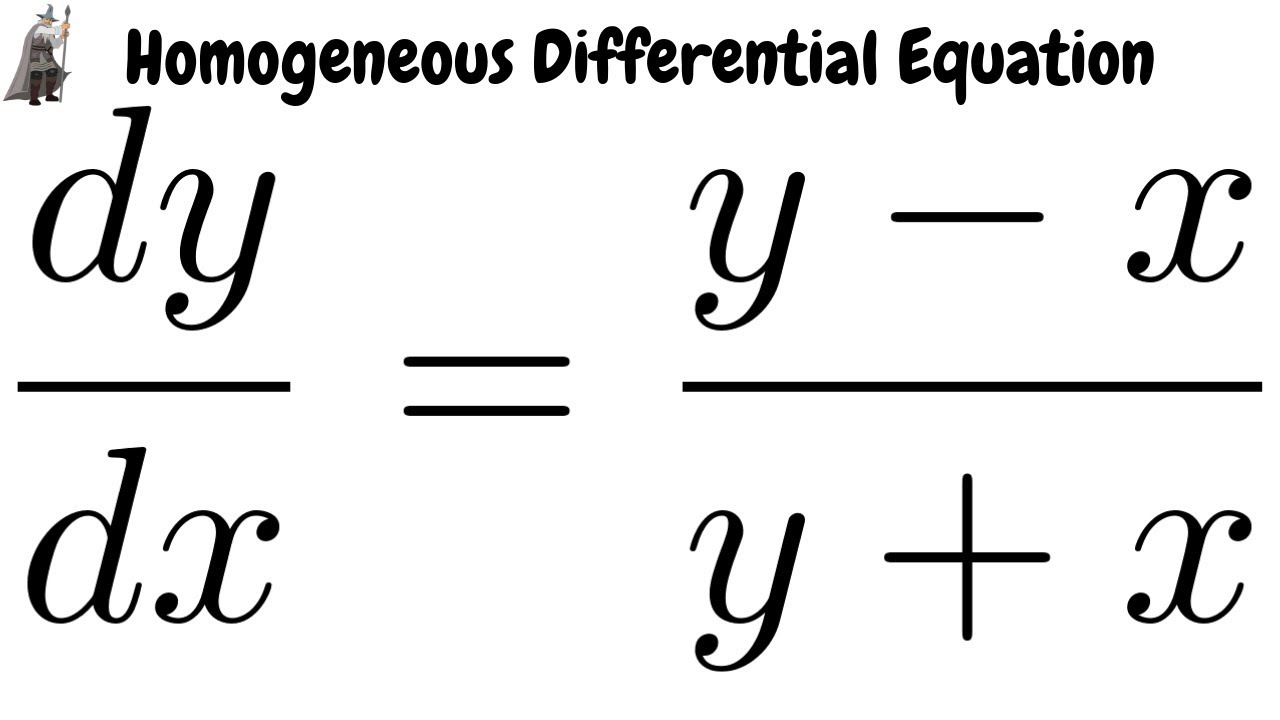
Solving The Homogeneous Differential Equation Dy Dx Y X Y X Youtube

Ex 5 5 15 Find Dy Dx Of Xy E X Y Class 12 Ex 5 5

Find Dy Dx For The Following I Y X 7 2 Ii

What Is The Derivative Of X Y Y X 11 Quora

Find The Particular Solution Of The Differential Equation X Y Dy Dx X 2y Given That Y 0 When X 1 Mathematics Shaalaa Com

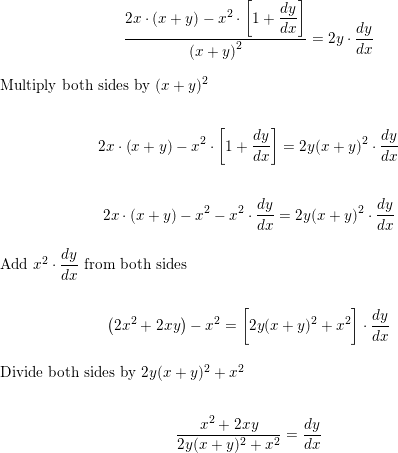
Find Dy Dx By Implicit Differentiation X2 X Y Y2 1 Homework Help And Answers Slader

1

X Y Y X 16 Find Dydx Maths Questions

Find Dy Dx For The Following Y X 7 2 Youtube

Problem Of The Day Calculator Allowed Ppt Download

If Y X 1 X Show That 2x Dydx Y 2 X

Ex 5 5 14 Find Dy Dx Of Cos X Y Cos Y X Logarithmic Different

Solution Solve The Linear Equation Dy Dx Y X X 2

7 Find Dy Dx By Implicit Differentiation X3 Y3 Gauthmath

What Is The Differentiation Of Y X 7 X 2 X 3 Quora

Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf

Find Dy Dx If X Y Y X A B Maths Limits And Derivatives Meritnation Com

How To You Find The General Solution Of Dy Dx X Y Socratic

2

If X2 Y2 2 Xy Find Dy Dx Mention Each And Every Step Mathematics Topperlearning Com Gwvwfskk

Ex 9 6 3 Find General Solution Dy Dx Y X X2 Ex 9 6

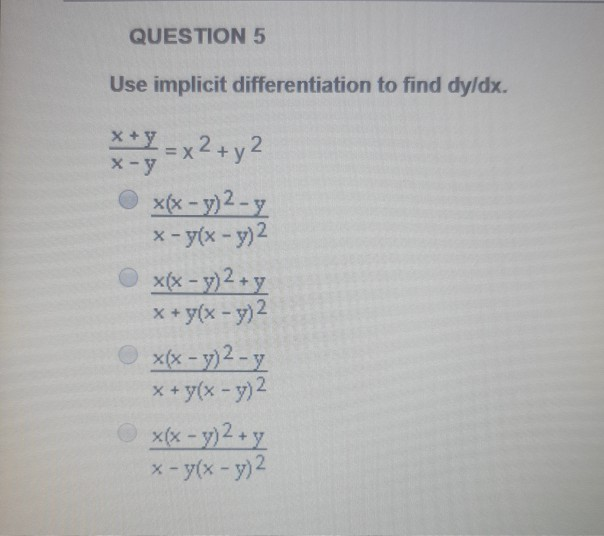
Question 5 Use Implicit Differentiation To Find Chegg Com

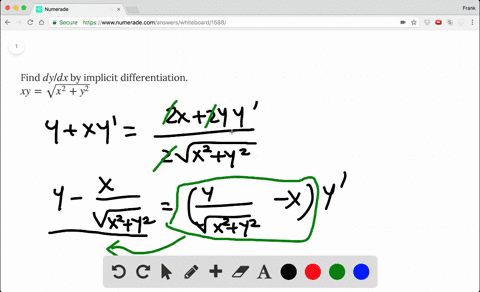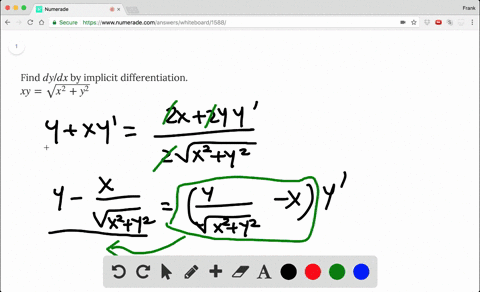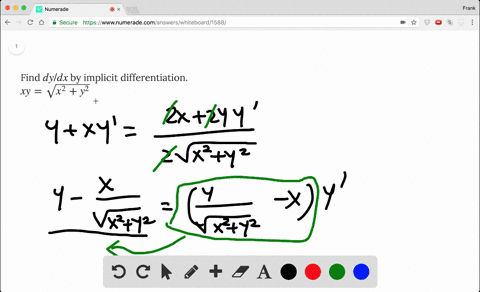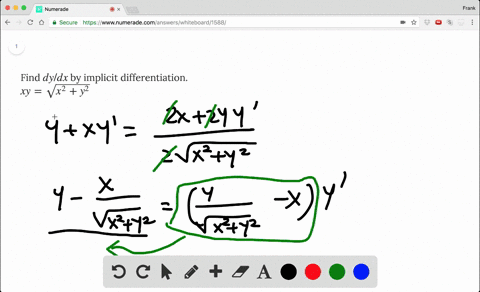
Solved Find Dy Dx By Implicit Differentiation Xy

Math 432 Hw 2 5 Solutions Pdf Free Download

Engineering Mathematics Notes

Math 113 Hw 7 Solutions

Ex 5 3 5 Find Dy Dx In X2 Xy Y2 100 Class 12

The Differential Equation X Dy Dx Y X 3 Has The General Solution Youtube

Math 432 Hw 2 5 Solutions Pdf Free Download

X X 1 Dy Dx X 2 Y X 3 2x 1 Novocom Top

Find Dy Dx If Y X Cot 1 X Y Brainly In

If X Y Y X 16 Then Dy Dx At 2 2 Is Maths Continuity And Differentiability Meritnation Com

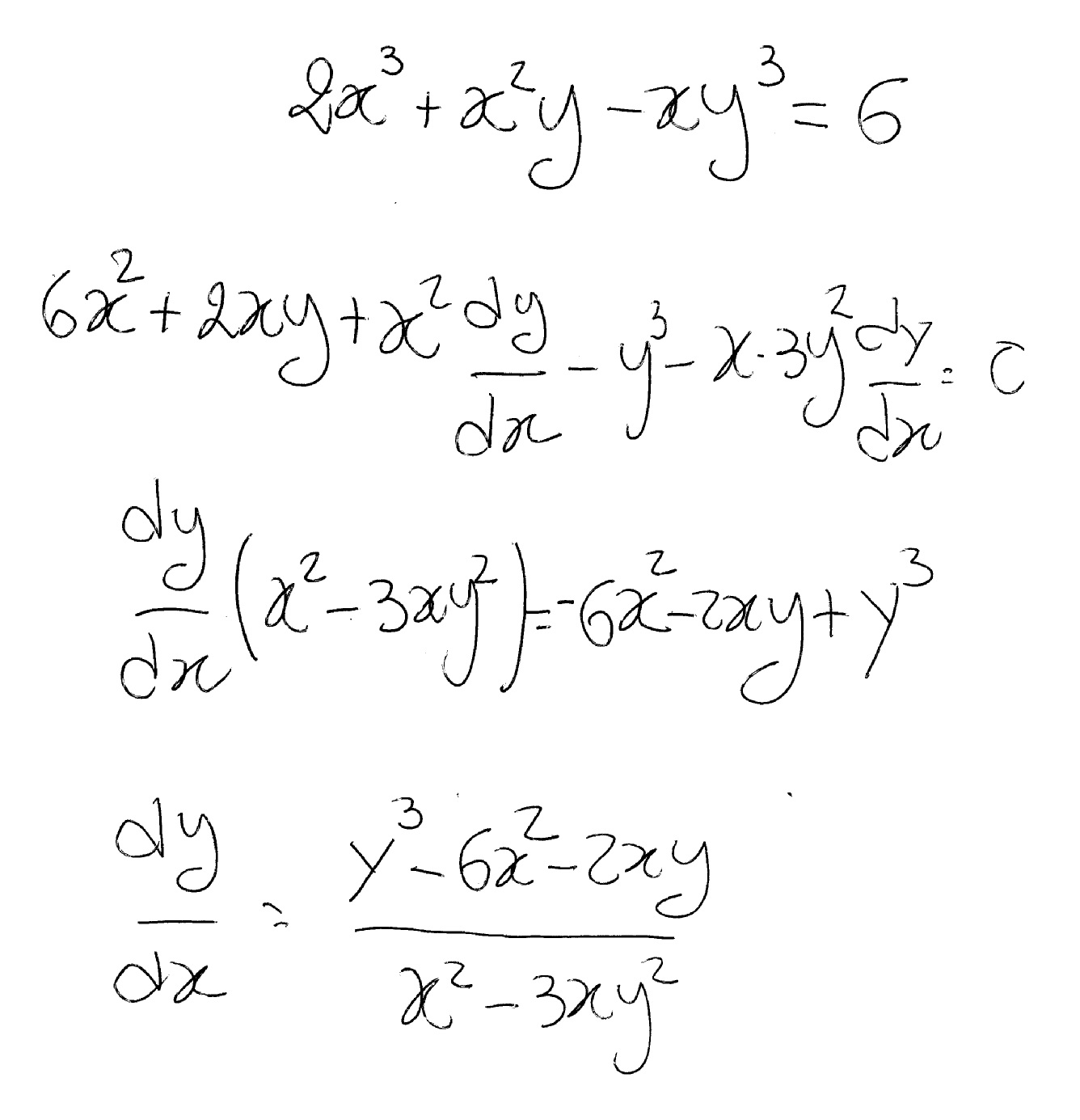
How Do You Find Dy Dx By Implicit Differentiation For 2x 3 X 2 Y Xy 3 6 Socratic

Www Tau Ac Il Levant Ode Solution 6 Pdf

X Tan Y X Y Dx Xdy 0 Novocom Top

3 8 Implicit Differentiation Calculus Volume 1

3 8 Implicit Differentiation Calculus Volume 1

Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com

Incoming Term: x^y+y^x=2 find dy/dx, if x^y+y^x=2 find dy/dx, example 9 if x^(y)+y^(x)=2 find (dy)/(dx), e 9 if x^(y)+y^(x)=2 find (dy)/(dx), if x^(y)+y^(x)=2 then find (dy)/(dx), example 9 quad if x^(y)+y^(x)=2 find (dy)/(dx), sin(xy)+x/y=x^2-y find dy/dx, if xy+(x)/(y)=x^(2)-y find (dy)/(dx), y=x^e^-x^2 find dy/dx, if sin(xy)+x/y=x^2-y find dy/dx,